
Poker Mathematics
Math is an integral part of the game of poker. Sure, in any one given trial, luck can play a role in defying the odds of any mathematical event taking place at the table. But in the long run, the math works itself out and the skill component of poker takes over.
In other words, you can’t take math out of poker. It is a part of the most basic building blocks in poker strategy, as well as all the way up to the most intricate, complex solutions being computed by powerful solvers and other studying aids available today.
As a member of the CLC community, you may be more aware of some of these components of the game. Access to solvers and other advanced studying programs is not all that hard to come by for those who are committed to improving their games.
However, if you don’t have a fundamental understanding of basic poker mathematics, you will only get so far in your poker journey, especially during in-game situations when access to additional tools is not readily available.
Keep reading below to learn about (or refresh yourself on) some of the most common and valuable situations in which you can apply poker math to your game.

Pot Odds
Simply put, pot odds allow you to calculate whether or not a decision is a profitable one. Every time you put chips into the pot, you are taking a calculated risk. For each decision you make, you must fold or choose to commit a certain amount of chips into the pot.
Of course, when you do that, there are already chips in the pot from the blinds and antes (and possibly other players entering the pot ahead of you). Pot odds are expressed in the form of a ratio, and that ratio is based on those exact factors we just mentioned: how much is in the pot and how much it costs you to call.
Let’s look at a basic example in a step-by-step manner:
We are in the big blind and commit 1bb preflop.
Another .5bb from the small blind and 1bb from the antes makes 2.5bb in the pot before any cards are dealt.
Say a player raises to 2bb from any position (not in the blinds) and action folds to us in the big blind. 2bb + 2.5bb already in the pot = 4.5bb.
Given that we have committed 1bb to the pot, it will cost us 1bb more to call.
Since pot odds are based on how much is in the pot (4.5bb) and how much it costs you to call (1bb), then we have 4.5-to-1 odds (also expressed as 4.5:1) to call.
What if we were in the small blind in this same example?
There’s still 2.5bb in the pot preflop plus another 2bb from the original raiser, totaling 4.5bb.
Since we put in .5bb from the small blind, that means it costs us 1.5bb to call.
Of course, 4.5-to-1.5 can be simplified to 3-to-1. Thus, our odds when facing a min-open in the small blind are 3-to-1 in this scenario.

Why Are Pot Odds Important?
Remember, we are technically taking a calculated risk whenever we commit chips to the pot. Often times this is important when facing a bet, as we can compare pot odds with equity and number of outs (more on that in a minute) in order to determine if a call is profitable, break-even, or losing money in the long run.
How exactly can we use pot odds to determine the profitability of a call?
Say we are facing a bet from our opponent on the flop while getting 4-to-1 odds with a draw. In order to break even, we’ll need to win 1 in 5 times at showdown, assuming no more chips go into the pot on further streets. If we are 30% to hit our draw and make the best hand in this scenario, we should basically never be folding.
Another common occurrence where pot odds come into play involves opening the action in a given pot by raising and then having an opponent re-jam. Let’s break this one down really quickly:
-
There’s 2.5bb in the pot from blinds and antes.
-
We raise to 2bb in the hijack and the cutoff jams for 8.5bb. Action folds back to us. What are our odds, and what % equity do we need to profitably call?
-
Initial 2.5bb + our 2bb open + 8.5bb re-jam = 13bb.
-
It costs us 6.5bb more to call, so 13bb divided by 6.5bb = 2-to-1 odds.
Of course, in this exact example, we will pretty much always be calling when laid 2-to-1 odds as our opening range will be strong enough to call when needing just 33% equity to break even.
One other important time in which to use pot odds is when we are the aggressor in a pot and are considering bet sizing. Based on the given dynamics of a certain hand, we will want to make sure we bet accordingly in order to give our opponent whatever odds we so desire.
-
For example, if there is 8bb in the pot and we bet 2bb, we are giving our opponent 5-to-1 odds to call (8bb + 2bb = 10bb in the pot, divided by the 2bb price to call).
-
If we bet 4bb in that same situation, we are giving our opponent 3to-1 odds to call (8bb + 4bb = 12bb in the pot, divided by the 4bb price to call).
-
A pot-sized bet of 8bb gives our opponent 2-to-1 odds (8bb + 8bb = 16bb, divided by 8bb to call).

Introducing Expected Value in Poker
Whatever odds we are getting, we can do our homework away from the tables and determine how our hand performs against opponents’ ranges from different positions and with different stack sizes. From there, we can do a math equation and figure out whether or not our call is profitable by comparing the Expected Value (EV) of all available options.
Looking at the example above, you will see that there can be situations where it is still profitable to call even as an underdog in the hand. If we are likely to win 40% of the time but only need to win 33% of the time to break even, it’s best to call.
Why? A simple EV calculation can answer this question.
A Simple EV Calculation
Consider the fact that we are presented with two options after raising and being faced with a re-jam.
We can fold, surrendering our 2bb.
We can call, risking 6.5bb more in order to win the 13bb that now totals the pot.
Math time: in Situation A, our net result is -2bb 100% of the time since we have committed 2bb to the pot and are now folding.
In Situation B, we risk 6.5bb more, bringing the total pot for grabs up to 19.5bb. Thus:
When we call and win (40% of the time): 19.5bb x 0.4 = 7.8bb
When we call and lose (60% of the time): -6.5bb x 0.6 = -3.9bb
The final part of this equation is to combine these two numbers: 7.8bb – 3.9bb = 3.9bb. Thus, calling an additional 6.5bb will net us a positive 3.9bb in the long run in this example where we are a 40% underdog preflop.
In the long run, these spots can really make a difference in your overall win rate. Be sure to know them thoroughly, as doing so will help you make better decisions at the table and ultimately make you more money. Master the Math. Dominate the Game.
Let CHIP LEADER AI do the heavy lifting—real-time odds, equity, and decision support from the minds behind Chip Leader Coaching.
Start using CLAI now and level up your edge.

Number of Outs, Equity, and Odds
Knowing your number of outs is necessary in order to calculate your equity, or the percentage of the time you will win a given pot. While you may already know how many outs many scenarios require in poker, there may also just be some complex situations in which you will have to think things through and simply count the number of cards that are outs.
Basic number-of-outs situations:
2 outs: KK vs AA
3 outs: AQ vs AK
4 outs: An inside/gutshot straight draw (i.e., 87 on a 952 flop)
5 outs: Middle pair vs. top pair (i.e., 87 vs AK on a K83 flop. Two remaining eights improve us to trips and an additional three sevens give us two pair.)
6 outs: Two overcards to a pair
8 outs: An open-ended straight draw (i.e., 87 on a 962 flop)
9 outs: A flush draw (i.e. 8c7c on a Ks3c2c flop. We have 4/13 clubs, meaning nine more remain in the deck for us to fill up.)
12 outs: A gutshot straight draw and flush draw (i.e., 8c7c on a Kc9c5d flop); one overcard and a flush draw
15 outs: An open-ended straight draw and flush draw (i.e., 8c7c on a 9c6c2h flop); two overcards and a flush draw
From there, you can compare your odds and equity to determine the EV of a decision. Some examples:
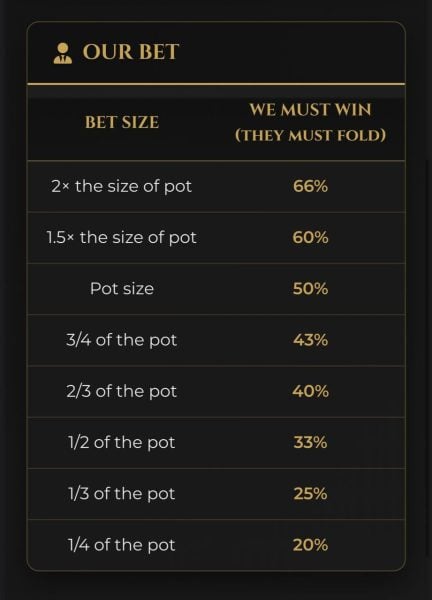
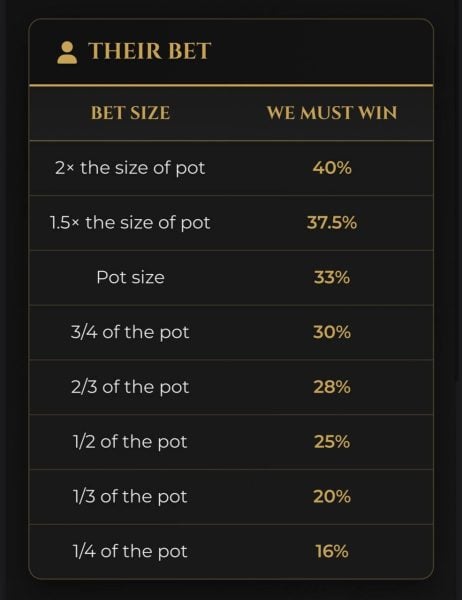
A bet size of 1/2 pot gives 3-to-1 odds, requiring 25% (1 in 4 times) to break even.
A bet size of 1/3 pot gives 4-to-1 odds, requiring 20% equity (1 in 5 times) to break even.
A bet of 1/4 pot gives 5-to-1 odds, requiring 16.66% equity (1 in 6 times) to break even.
See the pattern in these ratios? Whatever the denominator is in the fraction of a bet size related to the pot, the appropriate pot odds will be one number greater in its ratio.
Now that we’re clear on that, let’s talk percentages for a moment. The easiest way to calculate percentages on flops and turns for any number of outs is to multiply by 4x for the flop and 2x for the turn in order to see a rough likelihood of hitting one of your outs by the river.
As for exact percentages, we’ve compiled a chart and included it below for you to reference should you need to make a precise calculation:
Implied Odds
Implied odds are another concept within the umbrella of pot odds that can help you determine how much more you may win on future streets when hitting a hand such as a set or a straight/flush draw.
Remember when we talked about getting 2-to-1 odds and the like? Those are called expressed odds, referring directly to the situation at hand.
However, what happens when you are deep stacked and flop a big draw against a splashy player that is happy to put big bets into the middle? You know, the type of player that will give you his entire stack with an inferior hand when you hit?
That’s where implied odds come into play.
For example, say there is 8bb in the middle on the flop and we have a flush draw with 150bb effective stacks. If our opponent makes a pot-sized bet of 8bb, you are getting 2-to-1 expressed odds.
These odds are actually close to correct if we are sure our opponent will not put another chip into the middle on the turn or river, but this isn’t that type of opponent (and even if it was, we could never guarantee such a situation). By calling 8bb on the flop, we actually give ourselves a chance to take a much greater portion, if not all of our opponent’s stack on later streets when we hit; and as such, our implied odds might be 50-to-8 or 100-to-8 or 150-to-8, plenty good enough to see another street.
In other words, having good implied odds can make a situation much more favorable than it may appear on the surface based on direct pot odds.
It is also important to understand how board texture plays a role in implied odds, as a straight draw with 98 on a T72 board will be much more concealed than a flush on a four-spade board, for example.
Lastly, implied odds can play a role in a detrimental way, too. Reverse implied odds come into play in a situation where you could lose a lot (or all) of your chips even when you make a hand. Such occurrences happen when you run a set into a bigger set, a flush into a bigger flush, and so on. However, they can also happen in situations where you overplay a hand such as KQ on a K high board when deep stacked.

Postflop Probabilities
Postflop probabilities can help you understand how better to utilize pot odds in preflop situations. For example, knowing how often you will flop a flush (or flush draw) with two suited cards, will flop a set with a pocket pair, and so on, will help you utilize odds in order to make correct decisions more frequently.
Two major examples are as follows:
Suited cards will flop a flush less than 1% of the time and will make a flush just 6.5% of the time. While suited cards have much more playability than their offsuit counterparts, it’s important not to overestimate their strength.
A pair flops a set a little less than 1-in-8 times. This comes into play alongside implied odds: if you have a 15bb stack in middle position with 33 and a player raises to 2bb in early position, you do not have implied odds to make it profitable to hit your set, even if you got stacks in 100% of the time. (Given the fact you will not double up every time you flop a set, you may run it into a higher set, straight, flush, etc., your implied odds to set mine will actually need to be much greater than the given 8.33-to-1 in which you’ll hit.)

Conclusion
At its core, poker is a math game. Players who consistently win don’t rely on gut feeling—they use math to guide every decision.
By mastering pot odds, implied odds, equity, and EV, you’ll remove guesswork and emotion from your play. Over time, these skills will become second nature, helping you stay calm under pressure and spot profitable opportunities others miss.










